解析事例

間隙水圧を考慮した粒子-流体連成スキーム

1. はじめに

図-1に，2次元と3次元の場合について，このスキームを用いて粒子塊内に形成された流体格子（流体要素）を示します．球（3次元）あるいは円（2次元）で構成される粒子の集合体（粒子塊）内を，四面体（3次元）あるいは三角形（2次元）の流体格子で分割します．それぞれの流体格子は，お互いにその距離が最も近い粒子（4個の粒子：3次元，3個の粒子：2次元）の体積中心を結ぶことによって形成されます．流体格子は流体の貯留要素として，粒子間の間隙の幾何学形状と間隙に存在する流体の特性をあらわす要素です．間隙率と流体圧力（間隙水圧）は，流体格子の体積中心において定義され，それぞれの流体格子について流体の連続の式が満足されます．流体格子間は，その圧力差によって隣接する流体格子との境界より流体の出入りがあります．したがって，粒子の相対運動によって生ずる流体の圧縮性と流体格子境界からの流れによって各流体格子に発生する流体圧力が変化します．この流体圧力に流体格子内の間隙を形成する粒子の占有面積（濡れぶち）を乗じた力が体積力として粒子に作用します．なお個別要素法の接触はソフトコンタクト法を使っているため，粒子は剛体として扱われ粒子間のオーバーラップを許容します．したがって，粒子-流体連成スキームでの間隙の体積（面積）計算においても粒子間のオーバーラップが考慮されます．図2にこのスキームを用いて解析された地盤中を流れる水（地下水）の解析結果を示します．粒子間の間隙率の違いにより流れの局所化が再現できます．

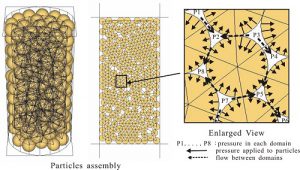
図-1　粒子塊中の間隙に生成される流体セル

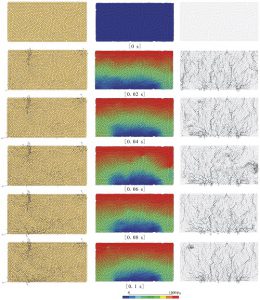
図-2　地盤中を流れる水（地下水）の解析：粒子の変位(左)，間隙水圧(中)，みかけ流速(左)

2. 土石流シミュレーション

図-3に，解析モデルを示します．解析モデルは，水路幅0.6m，全長8mの水平部と角度30度に傾斜した長さ4mの傾斜路，さらにその上部に土石流粒子を蓄える水密ゲートを設けた粒子貯蔵部を持つ実験装置の寸法諸元に合わせ，水平部と傾斜部それぞれを2次元の壁要素（線要素）を用い，またダム模型についても線要素を組み合わせて作成しました．粒子貯蔵部とダム部にそれぞれ,土石流と堆積土砂をモデル化した粒子が配置されます．ダム部に配置される粒子（堆積粒子）については，流下する粒子（土石流粒子）の衝突による挙動をわかり易くするために10cm x 10cmの矩形で色分けしました．

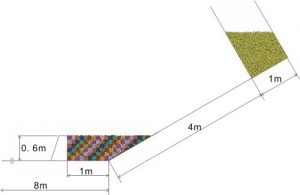
図-3　解析モデル（初期状態）

図-4に，ゲートに相当する壁を消去して1秒後から8 秒までの飽和状態（粒子-流体連成モデルがある場合）の土石流粒子と堆積粒子の運動状態を示します．飽和状態での計算結果は，土石流粒子がダム部堆積粒子に衝突したときに大きく跳ね上がり，その大きく跳ね上がった粒子がダムを超えて下流に運動していく傾向が顕著にあらわれます．また，土石流粒子が流下しダム部の堆積粒子に衝突し再び系が静定するまでの時間が長くなります．
図-5に，ゲートに相当する壁を消去して0.5秒後から8 秒までの，0.5秒ごとの飽和状態（粒子-流体連成モデルがある場合）のダム上流部での土石流粒子と堆積粒子内の間隙水圧の変化を示します．約1秒後に土石流粒子が堆積粒子に衝突し始めると，ダム上流部前方で間隙水圧が大きくなり始めその影響がダム上流部全体に広がっていきます．土石流粒子の衝突とその後の堆積粒子上部に上積みされた土石流粒子の影響で，ダム部堆積粒子内の間隙水圧は最下部を除いてほぼ全体にわたって上昇します．この傾向が粒子の運動がほぼ停止し堆積状態が静止したあとしばらく続き，その水圧は徐々に消散していき8秒後にはほぼ全体にわたって圧力は元の状態に戻ります．
図-6に，透水係数を図-5の条件の10倍にした場合の計算結果を示します．図-5の結果と比べると堆積粒子内に発生する過剰間隙水圧の値は小さく，圧力の上昇，消散の時間は短くなります．ゲートに相当する壁を消去してから約4秒で，上昇した間隙水圧は元の圧力に戻ります．また土石流粒子の衝突時の跳ね上がりは小さくなります．
過剰間隙水圧の発生で土石流土砂内部の有効応力が減少し抵抗力が小さくなるため，土石流土砂の流動化と高速長距離運動を引き起こし，ダムを越流する粒子が多くなると考えられます．

図-4　土石流粒子と堆積粒子の挙動 （飽和状態，1-8 sec)

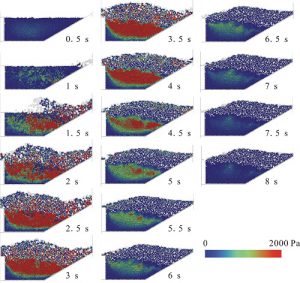
図-5　ダム上流部の土石流粒子と堆積粒子内の間隙水圧の変化 (透水係数1.2×10-2cm/s，0.5-8 sec)

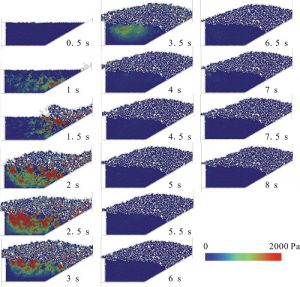
図-6　ダム上流部の土石流粒子と堆積粒子内の間隙水圧の変化（透水係数1.2×10-1cm/s，0.5-8 sec)

3. 液状化シミュレーション

図-7に解析モデル（(a) 粒子層と(b) 流体格子）を示します．粒子は，幅0.8mの矩形壁内に，高さ0.4mで作成されます．粒子は，奥行き0.2mの円柱形で，円形断面の平均粒子径は20mmで±20%の粒度分布をもたせました．2つの条件（緩んだ地盤：初期間隙率0.20，2次元，締まった地盤：初期間隙率0.16，2次元）についてモデルを作成しました．初期状態を作成した後，解析モデルに遠心模型実験に相当する条件で加振し，そのときの間隙水圧，有効応力ならびに粒子に作用する加速度を記録します．加振条件は，実地盤で200gal，1Hzの三角関数波を20波形（解析時間：5.0ないし25.0s）加えました．

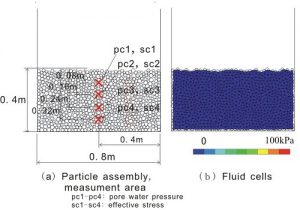
図-7　解析モデル

図-8に，初期間隙率0.20の場合の加振中（5.0ないし25.0s）の粒子層内の過剰間隙水圧の変化状況を示します．この場合には，加振が始まると粒子層内の各部で間隙水圧の変化がみられ，間隙水圧は徐々に大きくなります．粒子層上部とくらべ下部の間隙水圧の変化が大きくなります．また，間隙水圧の分布は水平方向にわたり均一ではなく局所的な違いがみられます．
図-9に，粒子層内の接触力の変化状況を示します．図中の黒線で示される粒子間の接触力は，その大きさに比例してその太さを変化させました．この場合には，加振前には，粒子の水中重量に対応する接触力が，粒子層の深さ方向に比例して増加する傾向がみられますが，振動が始まると粒子層上部のほうから徐々に粒子間力が小さくなることがわかります．また図-8の過剰間隙水圧分布の時間変化と比較すると，粒子層下部の接触力の大きい領域において，加振により過剰間隙水圧が大きくなり，液状化が進展し接触力が減少していく状況が観察されます．

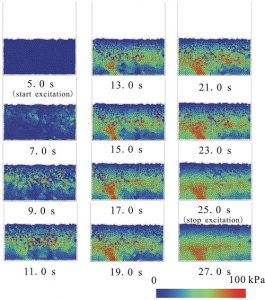
図-8　粒子層内の過剰間隙水圧の変化（緩んだ地盤：初期間隙率0.20）

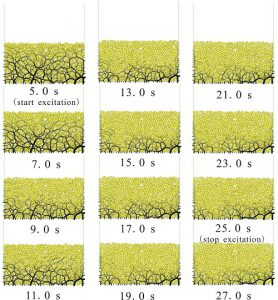
図-9　粒子層内の接触力の時間変化（緩んだ地盤：初期間隙率0.20）

参考文献

1). Shimizu, Y., Microscopic Numerical Model of Fluid Flow in Granular Material, Geotechnique, vol.61, no.10, pp.887-896, (2011)
2). Shimizu, Y. et al., A numerical simulation on centrifuge liquefaction model using microscopic fluid coupling scheme with Discrete Element Method, Proc. of 7th European Conf. on Numerical Methods in Geotechnical Eng., Trondheim, Norway, pp.201-206, (2010).
3). 清水 他，間隙水圧を考慮した粒子-流体連成モデルを用いた個別要素法による液状化解析，土木学会論文集C, vol.66, no.4, pp.800-813, (2010)
4). 清水 他，間隙水圧を考慮した粒子-流体連成モデルを用いた個別要素法による土石流シミュレーション，土木学会論文集C, vol.65, no.3, pp.633-643, (2009)