解析事例
粗流体格子粒子・流体連成スキーム
1. はじめに
粗流体格子粒子・流体連成スキームは,連続の式,運動量の式および熱エネルギーの式を粒子の存在を考慮しながら空間に固定されたそれぞれの流体セル(コントロールボリューム)ごとに圧力,流体速度ならびに温度を追跡する手法です.一方,流体セルに存在する粒子には,流体から推進力(抵抗力)が体積力として,また熱エネルギーが生成項として,それぞれ力と変位の法則および熱伝導の計算の中に組み込まれます.(図-1)
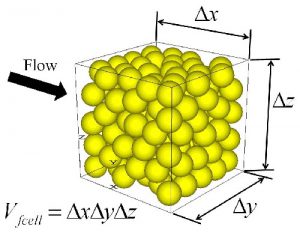
図-1 粒子塊の中を流れる熱流体
図-2に,粗流体格子粒子・流体連成スキームで生成される流体セル(2次元の場合)を示します.間隙率,圧力および流体温度がスカラーセルの中心部で定義されます.また運動量の式にはスタガードセルが用いられ,したがって流体速度はスカラーセルの境界で定義されます.さらに境界条件を考慮するために境界に余分な仮想セルが追加されます.
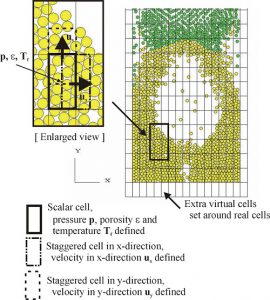
図-2 粒子塊(解析モデル)に設定された流体セル(2次元の場合)
図-3は,解析事例のひとつで,コンテナ内の粒子群の流動化シミュレーションの5秒間の時間変化を示したものです.粒子の色は,それぞれの粒子が持つ温度をあらわしています.図-4は,図-3の結果と比較するために,コンテナ内の粒子群を固定させて計算を行っています.図-3の場合には,流体が粒子を持ち上げ,コンテナ内で粒子群がよく混ざりあっています.同時に,流体からの熱エネルギーの移動(熱伝達)と粒子間の熱伝導により,コンテナ内の熱エネルギーの交換が良く行われているのがわかります.一方,固定粒子群の場合には,熱エネルギーが,流体注入部(下部中央)に集中していることがわかります.
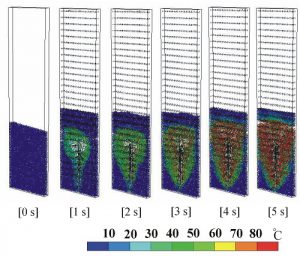
図-3 解析結果; 粒子の温度の時間変化と流体速度(流動化粒子の場合)
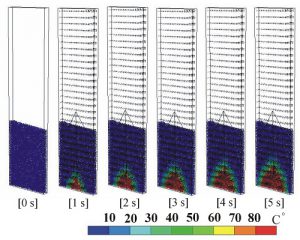
図-4 解析結果; 粒子の温度の時間変化と流体速度(固定粒子の場合)
2. メタンハイドレート資源開発への適用
粗流体格子粒子・流体連成スキームを,メタンハイドレート資源開発における回収時の生産システム配管内のメタンハイドレート粒子群の流動障害の検討に適用しました.適用にあたって,相変化(分解・生成)アルゴリズムと接着モデルを組み込みました. 図-5に,相変化モデルを示します.相変化により形成されたメタンハイドレート膜は,力学的な要因等で破壊され,新たなメタンガスと水の界面があらわれ,その反応が逐次進んでいくと考えられるが,その過程をモデリングすると計算が複雑となるので,ここでは,メタンハイドレート膜厚さが変化していくことで反応が進んでいくものと仮定しています.
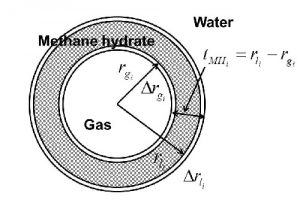
図-5 流動中のメタンハイドレート粒子の相変化(分解・生成)モデル
図-6にメタンハイドレートの相変化のアルゴリズム(フローチャート)を示します.まず,それぞれの流体セルの圧力と温度より,過冷却状態かあるいは,メタンガス・水が安定に存在する領域かどちらかの判定を行い,以下の過程で計算を進めます.
過冷却状態の場合には,その流体セル内のすべての粒子について,粒子すべてあるいは一部分が気体(メタンガス)であるかどうかチェックします。もしメタンガスが存在していなければ,その粒子は,メタンハイドレートだけの成分の粒子であるので相変化は起こりません.もしメタンガスが存在していれば,メタンガスと水からメタンハイドレートへ相変化するときの質量変化量を求め,相変化による間隙率変化,メタンハイドレートの厚さおよび離散相の密度,さらに潜熱による熱エネルギーを計算します.この相変化による間隙率変化ならびに潜熱による熱エネルギーの生成項を,流体計算における質量保存式ならびに熱エネルギー保存式に組み込みます.
一方,メタンガス・水の安定領域の場合には,粒子すべてあるいは一部がメタンハイドレートであるかどうかチェックします.もしメタンハイドレートが存在していない,すなわちメタンガスだけで構成される粒子であれば,圧力と温度変化にともなうメタンガス粒子径を変更し,体積変化を流体計算における質量保存式の中に組み込みます.メタンハイドレートが存在している場合には,メタンハイドレートからメタンガスと水への相変化が起こりますから,その計算の過程は,過冷却状態でメタンガスが存在している場合と同じロジックを用います.
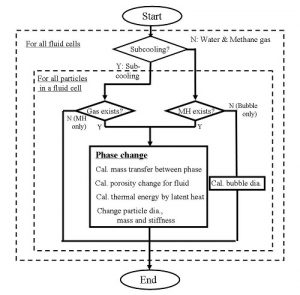
図-6 相変化アルゴリズムのフローチャート
生成したメタンハイドレート粒子は,粒子濃度が大きい場合には粒子同士が凝集,あるいは構成機器内部に付着すると考えられます.そこで,個別要素法の粒子運動計算の中に,粒子同士が接触あるいは粒子が壁に接触したときに接着力を作用させるようにしました(図-7).この接着力は,接触面に対して垂直方向(引張)と接触面の方向(せん断)に対する抵抗力としてあらわされるだけでなく,曲げあるいはねじりに対しても抵抗力をあらわすようにしました.
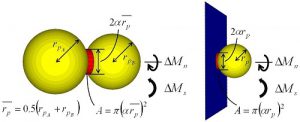
図-7 接着力モデル
メタンハイドレート資源を減圧法で採取するための構成機器内部の流動障害の検討を目的として,坑井の水位低下の目的で使用される配管(水平ダクト)内部のシミュレーション(図-8: 解析モデル)を行いました.図-9は,矩形ダクト内を流動する接着力を有する粒子群について,解析モデルの中央部分(図-8中の赤く示した矩形領域)の間隙率εおよび測定領域を上下方向に4つの領域に分割し,それぞれの領域での間隙率(下からε1, ε2, ε3, ε4)の時間変化を示します。計算が開始すると,解析領域内に均等に分布していた粒子群が流れの方向に進行しながら徐々に上部に移動し,開始から2秒ほどでほぼ矩形ダクトの上部に集積しながら移動します.接着力がある場合の流動では,解析領域中央部の間隙率濃度の時間変化がみられ,粒子がお互いに接着して塊となって流動していく状態が再現できます.このように,粒子間あるいは粒子-壁間に接着力を付加することにより,時間の経過とともに粒子群はお互いに接着しダクト内の間隙率分布が変動し,接着モデルが粒子間の凝集を再現できることがわかりました.

図-8 解析モデル
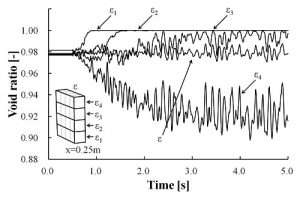
図-9 計算結果(接着力がある粒子群)
参考文献
1). Shimizu, Y., Three-Dimensional Simulation Using Fixed Coarse-Grid Thermal-Fluid Scheme and Conduction Heat Transfer Scheme in Distinct Element Method, Powder Technology, vol.165, pp.140-152, (2006). 2). 清水 他,メタンハイドレート資源開発における坑井内流動障害に関する数値計算 - 相変化を考慮した個別要素法による粗流体格子粒子-熱流体連成モデルの開発 -,資源・素材学会誌,Vol. 129, pp11-20, (2013).