イタスカジャパン Itasca Japan 地球科学・地球工学分野の数値解析コード開発・解析業務

解析事例

格子ボルツマン法と個別要素法の連成スキーム

1. はじめに

格子ボルツマン法は，流体解析においてNavier-Stokesの方程式を直接解かずに，仮想粒子の分布関数により解を得る手法です．この２次元格子ボルツマン法を，埋め込み移動境界法を用いて個別要素法と連成させることにより，例えば地盤材料内の流体流れに伴う砂粒子の挙動をシミュレーションすることができます．ここでは，2次元9速度モデルを用いました（図-1）．

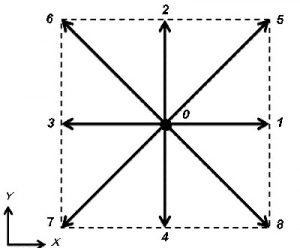
図-1　２次元９速度モデル

2. 流体解析

２次元格子ボルツマン法による流体計算の精度検証として，Cavity流れの計算結果を示します．格子ボルツマン法の計算精度は，計算パラメータならびに時間緩和係数と境界条件に依存することがわかりました．計算結果は，比較するための数値計算解(Ghia et al.,1982)に近い結果が得られました．

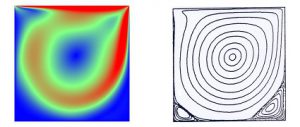
図-2　計算結果（左：速度コンター）と比較のための数値計算結果（右：Ghia et al.,1982)

3. 粒子運動（個別要素法）との連成

２次元格子ボルツマン法および連成解析手法の解析例として，地盤材料内における粒子（細粒砂）運動を伴う流体計算を行いました．図-3および図-4は，間隙率を同じにしてそれぞれ地盤材料の構造（固定粒子（灰色）の配置）を変えた条件で，左側から細粒砂（黄色）を加えた場合の，流体の圧力および速度コンターと細粒砂の地盤材料内での堆積状況を示します．同じ間隙率であっても地盤材料の構造（固定粒子の配置）の違いによって，細粒砂の挙動や流体の流れやすさ（浸透率）が異なることを再現できます．

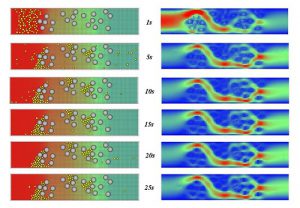
図-3　圧力・速度コンター(固定粒子配置パターン0，細粒砂粒子濃度30％)

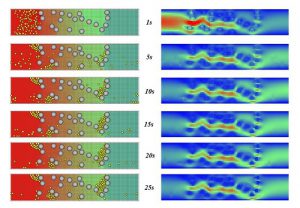
図-4　圧力・速度コンター(固定粒子配置パターン1，細粒砂粒子濃度30％)

参考文献